Shape Selection and Representation



Shape Selection and Representation

Among vision research, there are two important questions. One is the salience problem, trying to derive depth information from images. Another is the categorization problem, trying to matching a candidate figure to a ideal prototype in our trained memory. To detect the illusory contours is a trial on the road to solve the salience problem.

We use some synthesized images here as source images to illustrate the idea.

The well-known image in many illusory contours experiments, the Kanizsa Square is for demonstrating the idea of multilayers and amodal completion. The 4 Crosses suggests different illusory phenomenon, no salient square in the middle. This result suggests the priori with smooth contours for salient figures. Therefore, number of corners is an important issue in selecting the winning visual organization. The 2 Fish is a more complicated case as two figures each has part of it occluded by another.

Summarily, we are interested in some topics:

1. Illusory figure finding,
We try to detect the illusory surface in synthesized images. Our approach combines the segmentation as an intergal part of our salient-surface finding process.

2. Figure/background separation,
We try to use perceptual data as inspiration to build a model which can be useful as part of the general vision recognition engine.

3. Shape Analysis,
We try to obtain some structure and measurement to describe general shapes. Some well-known measurement are convexity, symmetry, size, and parallelism, etc.

Publications:

A Continuous Shape Descriptor by Orientation Diffusion, H. K. Pao and D. Geiger,
The 3rd International Workshop on EMMCVPR,
September 2001, France.

Measuring Convexity for Figure/Ground Separation, H. K. Pao, D. Geiger and N. Rubin,
IEEE International Conference on Computer Vision,
September 1999, Kerkyra, Greece.

The Shape of Illusory Figures, D. Geiger, Krishnan Kumaran, H . K. Pao and N. Rubin,
IEEE Signal Processing Society, International Conference on Image Processing,
October 1999, Kobe, Japan.

Salient and Multiple Illusory Surfaces, D. Geiger, H. K. Pao and N. Rubin,
IEEE Computer Society Conference on Computer Vision and Pattern Recognition,
June 1998, Santa Barbara, CA.

Experimental Images and Results:

A. Convexity for Foreground/Background Separation
(in the diffusion here, white indicates "on top" and black indicates "below")

Original Image

diffusion with smaller decay

diffusion with larger decay

iso-contours

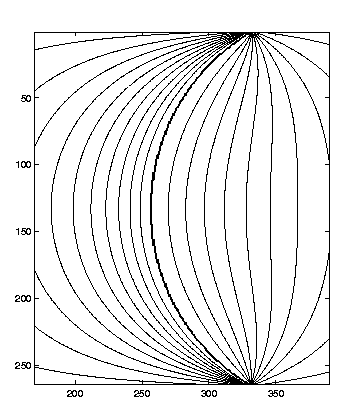
A1. The idea of convexity modeling by decay diffusion process

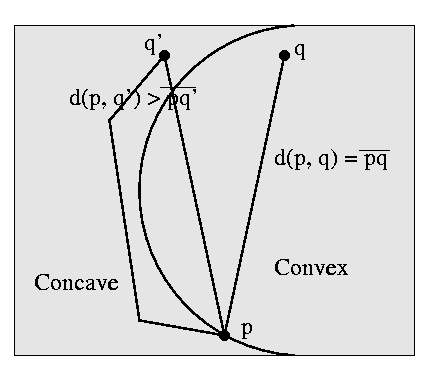
In the graph, the right/left side shows the convex/concave side and they are blocked by intensity edges (it will serve as inducers) in the middle. The situation d(p,q') > d(p,q) favors the convex side because the energy in the decay diffusion process will decay as the walking distance (from the inducers) become larger. The diffusion result is shown above and below. We got a steeper gradient in the concave side and smoother gradient in the convex side.

A2. Convexity vs Symmetry
(adapted from Kanizsa's "Organization in Vision", Praeger, New York, 1979.)

Convexity in black

Convexity in white

Diffusion

B. Illusory Contours and Amodal Completion
(in sparse data and diffusion, white indicates "on top" and black indicates "below")

Kanizsa Square	Top	Occluded
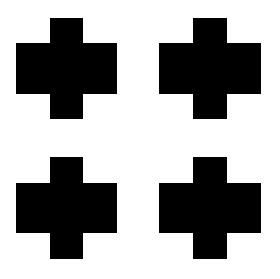Four Crosses	Top	Occluded
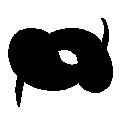Two Fish	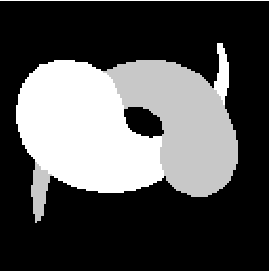Amodal Completion	Occluded